RANGKAIAN RESONANSI RLC KOMBINASI
Kelompok 3 : - M. Ibnu Fahridho (14)
- Salsha Afifa R (21)
Kelas : EC 2C
Mata kuliah : Rangkaian Listrik Lanjut
RANGKAIAN RLC
Rangkaian RLC adalah
rangkaian yang tersusun atas resitor, induktor, dan kapistor baik secara seri
maupun paralel. Rangkaian ini dinamakan RLC karena menunjukkan simbol ketahanan
(R), induktansi (L), dan kapasitansi (C). Rangkaian RLC bisa membentuk osilator harmonik dan akan
beresonansi pada rangkaian LC
1. Arus AC (arus bolak-balik)
pada resistor
Arus AC sebesar I yang
melewati resistor akan muncul tegangan seperti persamaan berikut.
Dari persamaan tersebut
terlihat bahwa besarnya arus yang melalui resistor sebandingan dengan tegangan
yang dihasilkan. Artinya, jika arus yang masuk besar, tegangan yang dihasilkan
juga akan besar. Keadaan itu dikatakan bahwa arus dan tegangannya sefase. Perhatikan
grafik berikut.
2. Arus AC (arus bolak-balik) pada induktor
Jika suatu induktor dilalui arus AC yang besarnya berubah setiap waktu, maka akan dihasilkan tegangan induksi VL. Secara matematis, hubungan antara arus dan tegangan induksi dirumuskan sebagai berikut
Semakin besar perubahan arus setiap waktu, semakin
besar pula tegangan induksinya. Tegangan induksi akan muncul setelah ada
perubahan arus pada selang waktu tertentu. Dari kondisi tersebut, bisa
dikatakan bahwa jalannya arus tidak serentak dengan tegangan atau tegangan
tidak sefase dengan arus. Tegangan akan mendahului arus dengan beda sudut fase 90°
Gambar
paling kiri merupakan contoh susunan induktor, gambar tengah merupakan grafik
sinusoidal antara tegangan dan arus, serta gambar paling kanan merupakan
diagram fasor antara tegangan dan arus. Pada gambar tengah terlihat bahwa
tegangan mendahului arus dengan beda sudut fase 90o atau
arus tertinggal tegangan sejauh 90°.
3.
Arus AC (arus bolak-balik) pada kapasitor
Saat
kapasitor dilalui Arus AC sebesar IC, akan muncul tegangan VC. Tegangan kapasitor tersebut akan naik
menjadi Vt secara perlahan. Secara matematis,
dirumuskan sebagai berikut.
Saat kapasitor dilalui arus, tegangan kapasitor akan naik. Sebaliknya, saat arus diturunkan sampai ke titik nol, tegangan kapasitor akan turun secara perlahan. Keadaan ini menunjukkan bahwa arus dan tegangan tidak berjalan secara serempak. Artinya, arus dan tegangan tidak sefase. Arus akan mendahului tegangan dengan beda sudut fase 90°.
Gambar paling kiri merupakan contoh susunan kapasitor, gambar tengah merupakan grafik sinusoidal antara tegangan dan arus, serta gambar paling kanan merupakan diagram fasor antara tegangan dan arus. Pada gambar tengah terlihat bahwa arus mendahului tegangan dengan beda sudut fase 90o atau tegangan tertinggal arus sejauh 90°
.
Dalam rangkaian RLC seri terdapat titik frekuensi di mana reaktansi induktif induktor menjadi sama nilainya dengan reaktansi kapasitif kapasitor. Dengan kata lain, XL = XC. Titik di mana hal ini terjadi disebut titik Frekuensi Resonansi, ( ƒr ) dari rangkaian, dan ketika kami menganalisis rangkaian RLC seri, frekuensi resonansi ini menghasilkan Resonansi Seri.
Rangkaian Resonansi Seri adalah salah satu rangkaian terpenting yang digunakan dalam rangkaian listrik dan elektronik. Mereka dapat ditemukan dalam berbagai bentuk seperti pada filter listrik AC, filter kebisingan dan juga di rangkaian penyetelan radio dan televisi menghasilkan rangkaian penyetelan yang sangat selektif untuk menerima saluran frekuensi yang berbeda. Pertimbangkan rangkaian RLC (Resistor, Induktor, dan Kapasitor) seri sederhana di bawah ini.
Namun, ketika frekuensi mendekati nol atau DC, reaktansi induktor akan
berkurang menjadi nol, menyebabkan efek sebaliknya bertindak seperti korsleting.
Ini berarti bahwa reaktansi induktif adalah “ Proporsional ” terhadap frekuensi
dan kecil pada frekuensi rendah dan tinggi pada frekuensi lebih tinggi dan ini
ditunjukkan dalam kurva berikut:
Reaktansi
Induktif Terhadap Frekuensi
Grafik reaktansi induktif terhadap frekuensi adalah kurva garis lurus. Nilai reaktansi induktif dari sebuah induktor meningkat secara linear seiring dengan meningkatnya frekuensi yang melintasi induktor. Oleh karena itu, reaktansi induktif adalah positif dan berbanding lurus dengan frekuensi ( XL ∝ ƒ )
Hal yang sama juga berlaku untuk rumus reaktansi kapasitif di atas tetapi secara terbalik. Jika Frekuensi atau Kapasitansi ditingkatkan, keseluruhan reaktansi kapasitif akan berkurang. Ketika frekuensi mendekati tak terbatas, reaktansi kapasitor akan berkurang menjadi nol sehingga elemen rangkaian bertindak seperti konduktor sempurna 0Ω.
Tetapi ketika frekuensi mendekati tingkat nol atau DC, reaktansi kapasitor akan
dengan cepat meningkat hingga tak terbatas yang menyebabkannya bertindak
seperti resistansi yang sangat besar, menjadi lebih seperti kondisi rangkaian
terbuka.
Ini berarti bahwa reaktansi kapasitif adalah " Berbanding terbalik "
dengan frekuensi untuk setiap nilai kapasitansi yang diberikan dan ini
ditunjukkan di bawah ini:
Grafik reaktansi kapasitif terhadap frekuensi adalah kurva hiperbolik. Nilai Reaktansi dari sebuah kapasitor memiliki nilai yang sangat tinggi pada frekuensi rendah tetapi dengan cepat berkurang dengan meningkatnya frekuensi. Oleh karena itu, reaktansi kapasitif negatif dan berbanding terbalik dengan frekuensi ( XC α ƒ-1 )
Kita dapat melihat bahwa nilai-nilai resistansi ini tergantung pada frekuensi supply. Pada frekuensi yang lebih tinggi XL tinggi dan pada frekuensi rendah XC tinggi. Maka harus ada titik frekuensi dimana nilai XL sama dengan nilai XC dan ada.
Jika sekarang kita menempatkan kurva untuk reaktansi induktif di atas kurva untuk reaktansi kapasitif sehingga kedua kurva pada sumbu yang sama, titik persimpangan akan memberi kita titik resonansi seri frekuensi, ( ƒr atau ωr ) seperti yang ditunjukkan di bawah ini .
di mana: ƒr di Hertz, L di Henries dan C di Farads.
Resonansi listrik terjadi dalam rangkaian AC ketika dua reaktansi yang berlawanan dan sama-sama membatalkan satu sama lain sebagai XL = XC dan titik pada grafik di mana ini terjadi adalah dua kurva reaktansi saling bersilangan. Dalam sebuah rangkaian resonanai seri, frekuensi resonansi, ƒr titik dapat dihitung sebagai berikut.
Kita bisa melihat kemudian bahwa pada resonansi,
dua reaktansi membatalkan satu sama lain sehingga membuat kombinasi LC
seri bertindak sebagai rangkaian pendek dengan perlawanan hanya untuk
aliran arus dalam rangkaian resonansi seri menjadi resistansi, R.
Dalam bentuk yang kompleks, frekuensi resonansi
adalah frekuensi di mana total impedansi rangkaian RLC seri menjadi murni
"nyata", yang tidak ada impedansi imajiner. Ini karena pada resonansi
mereka dibatalkan. Jadi total impedansi dari rangkaian seri menjadi hanya nilai
resistansi dan karena itu: Z = R.
Kemudian pada resonansi impedansi rangkaian seri berada pada nilai minimum dan hanya setara dengan resistansi, R dari rangkaian. Impedansi rangkaian pada resonansi disebut "impedansi dinamis" rangkaian dan tergantung pada frekuensi, XC (biasanya pada frekuensi tinggi) atau XL (biasanya pada frekuensi rendah) akan mendominasi kedua sisi resonansi seperti ditunjukkan di bawah ini.
Impedansi dalam Rangkaian Resonansi Seri
Perhatikan bahwa ketika reaktansi kapasitif mendominasi rangkaian kurva impedansi memiliki bentuk hiperbolik untuk dirinya sendiri, tetapi ketika reaktansi induktif mendominasi rangkaian kurva adalah non-simetris karena respon linear dari XL.
Anda juga dapat mencatat bahwa jika impedansi rangkaian pada resonansi minimum maka akibatnya, admitansi/penerimaan rangkaian harus pada maksimum dan salah satu karakteristik dari rangkaian resonansi seri adalah bahwa admitansi sangat tinggi.
Tetapi ini bisa menjadi hal yang buruk karena nilai resistansi yang sangat rendah pada resonansi berarti bahwa arus yang dihasilkan yang mengalir melalui rangkaian mungkin sangat tinggi. Kita ingat dari tutorial sebelumnya tentang rangkaian RLC seri bahwa tegangan kombinasi seri adalah jumlah fasor dari VR, VL dan VC.
Kemudian jika di resonansi dua reaktansi adalah sama dan membatalkan, dua tegangan yang
Kemudian dalam rangkaian resonansi seri sebagai VL = -VC tegangan reaktif yang dihasilkan adalah nol dan semua tegangan supply dijatuhkan melintasi resistor. Oleh karena itu, VR = Vsupply dan untuk alasan inilah rangkaian resonansi seri dikenal sebagai rangkaian resonansi tegangan, (berlawanan dengan rangkaian resonansi paralel yang merupakan rangkaian resonansi arus).
Rangkaian RLC Seri pada Resonansi
Karena arus yang mengalir melalui rangkaian resonansi seri
adalah hasil tegangan dibagi dengan impedansi, pada resonansi impedansi, Z
adalah pada nilai minimumnya, ( =R ). Oleh karena itu, arus rangkaian pada
frekuensi ini akan berada pada nilai maksimum V/R seperti yang ditunjukkan di
bawah ini.
Arus Rangkaian pada Resonansi Seri
Kurva respons frekuensi dari rangkaian resonansi seri
menunjukkan bahwa besarnya arusadalah fungsi frekuensi dan memplotnya ke grafik menunjukkan
kepada kita bahwa respons dimulai dari mendekati nol, mencapai nilai maksimum
pada frekuensi resonansi ketika IMAX = IR dan kemudian turun lagi ke hampir nol ketika ƒ menjadi tidak
terbatas.
Hasil dari ini adalah bahwa besarnya tegangan melintasi induktor, L dan
kapasitor, C dapat menjadi berkali-kali lebih besar dari tegangan supply,
bahkan pada resonansi tetapi karena mereka sama dan pada perlawanan mereka
membatalkan satu sama lain.
Karena rangkaian resonansi seri hanya berfungsi pada frekuensi resonansi, rangkaian jenis ini juga dikenal sebagai Rangkaian Akseptor karena pada resonansi, impedansi rangkaian minimum, sehingga dengan mudah menerima arus yang frekuensinya sama dengan frekuensi resonansinya.
Anda juga dapat memperhatikan bahwa karena arus maksimum melalui rangkaian pada resonansi hanya dibatasi oleh nilai resistansi (nilai murni dan nyata), maka tegangan sumber dan arus rangkaian harus dalam-fasa satu sama lain pada frekuensi ini.
Kemudian sudut-fasa antara tegangan dan arus rangkaian resonansi seri juga
merupakan fungsi frekuensi untuk supply tegangan tetap dan yang nol pada
titik frekuensi resonansi ketika: V, I dan VR semuanya dalam-fasa satu sama lain seperti ditunjukkan di
bawah ini. Akibatnya, jika sudut fasa adalah nol maka faktor daya karena itu
harus bersatu.
Sudut Fasa dari
Rangkaian Resonansi Seri
Perhatikan juga, bahwa sudut fasa positif untuk frekuensi di atas ƒr dan negatif untuk frekuensi di bawah ƒr dan ini dapat dibuktikan dengan,
Bandwidth dari Rangkaian Resonansi Seri
Jika rangkaian RLC seri digerakkan oleh frekuensi variabel pada
tegangan konstan, maka besarnya arus, I sebanding dengan
impedansi, Z, oleh karena itu pada resonansi daya yang diserap oleh
rangkaian harus pada nilai maksimumnya sebagai P = I2Z.
Jika kita sekarang mengurangi atau meningkatkan frekuensi hingga daya rata-rata yang diserap oleh resistor dalam rangkaian resonansi seri adalah setengah dari nilai maksimumnya pada resonansi, kami menghasilkan dua titik frekuensi yang disebut titik setengah daya yang -3dB turun dari maksimum, mengambil 0dB sebagai referensi arus maksimum.
Titik-titik 3dB memberi kita nilai arus yang 70,7% dari nilai
resonansi maksimum yang didefinisikan sebagai: 0,5(I2R) = (0,707 x I)2R. Maka titik sesuai dengan frekuensi yang
lebih rendah di setengah daya disebut “lower frekuensi cut-off”, label ƒL dengan titik
sesuai dengan frekuensi atas di setengah daya yang disebut “upper cut-off
frekuensi”, berlabel ƒH.
Jarak antara dua titik ini, yaitu ( ƒH - ƒL ) disebut Bandwidth, (BW) dan merupakan rentang frekuensi di
mana setidaknya setengah dari daya maksimum dan arus disediakan seperti yang
ditunjukkan.
Bandwidth dari Rangkaian
Resonansi Seri
Respons frekuensi dari besaran arus rangkaian di atas,
berhubungan dengan “ketajaman” resonansi dalam rangkaian resonansi seri.
Ketajaman puncak diukur secara kuantitatif dan disebut faktor Kualitas, Q dari
rangkaian.
Faktor kualitas menghubungkan energi maksimum atau puncak yang disimpan dalam
rangkaian (reaktansi) dengan energi yang dihamburkan (resistansi) selama setiap
siklus osilasi yang berarti bahwa itu adalah rasio frekuensi resonansi terhadap
bandwidth dan semakin tinggi rangkaian Q, semakin kecil bandwidth, Q = ƒr/BW.
Selektivitas dari rangkaian resonansi seri dapat dikendalikan dengan
menyesuaikan nilai resistansi saja, menjaga semua komponen lain yang sama,
karena Q = (XL atau XC) / R .
Bandwidth dari Rangkaian Resonansi RLC Seri
Kemudian hubungan antara resonansi, bandwidth, selektivitas dan
faktor kualitas untuk rangkaian resonansi seri didefinisikan sebagai:
1). Frekuensi resonansi, ( ƒr )
2). Arus, ( I )
3). Frekuensi cut-off yang lebih rendah, ( ƒL )
4). Frekuensi cut-off atas, ( ƒH )
5). Bandwidth, (BW)
RANGKAIAN RESONANSI RLC PARALEL
Rangkaian resonansi paralel dipengaruhi oleh arus yang mengalir melalui masing-masing cabang paralel dalam rangkaian tangki LC paralel. Sebuah rangkaian tangki adalah kombinasi paralel dari L dan C yang digunakan dalam jaringan penyaring baik pilih atau menolak frekuensi AC
Mari kita mendefinisikan apa yang sudah kita ketahui tentang rangkaian RLC paralel.
Rangkaian
paralel yang berisi Resistor R, Induktor, L, dan Kapasitor, C akan menghasilkan
rangkaian resonansi paralel (disebut anti-resonansi)
ketika arus yang dihasilkan melalui kombinasi paralel dalam-fasa dengan
tegangan supply. Pada resonansi akan ada arus sirkulasi besar antara induktor
dan kapasitor karena energi osilasi, maka rangkaian paralel menghasilkan
resonansi arus.
Sebuah rangkaian resonansi paralel menyimpan
energi rangkaian di medan magnet dari induktor dan medan listrik dari
kapasitor. Energi ini terus-menerus dipindahkan bolak-balik antara induktor dan
kapasitor yang menghasilkan arus nol dan energi ditarik dari supply. Hal ini
karena sesuai nilai-nilai sesaat dari IL dan IC akan selalu sama dan
berlawanan dan karena arus yang ditarik dari supply adalah penjumlahan
vektor dari dua arus ini dan arus yang mengalir di IR.
Dalam solusi rangkaian resonansi paralel AC kita
tahu bahwa tegangan supply umum untuk semua cabang, jadi ini dapat diambil
sebagai vektor referensi kami. Setiap cabang paralel harus diperlakukan secara
terpisah seperti rangkaian seri sehingga total arus supply yang diambil oleh
rangkaian paralel adalah penambahan vektor dari arus cabang individu.
Lalu ada dua metode yang tersedia bagi kita
dalam analisis rangkaian resonansi paralel. Kami dapat menghitung arus di
setiap cabang dan kemudian menambahkan bersama-sama atau menghitung admitansi
dari masing-masing cabang untuk menemukan arus total. Kita tahu dari sebelumnya
resonansi seri yang resonansi terjadi ketika VL = -VC dan situasi ini terjadi
ketika dua reactances adalah sama, XL = XC. Admitansi dari rangkaian paralel diberikan
sebagai:
Resonansi terjadi ketika XL = XC dan bagian imajiner dari Y menjadi nol. Kemudian:
Perhatikan
bahwa pada resonansi, rangkaian paralel menghasilkan persamaan yang sama
seperti untuk rangkaian resonansi seri. Oleh karena itu, tidak ada bedanya jika
induktor atau kapasitor dihubungkan secara paralel atau seri.
Juga pada resonansi, rangkaian tangki
LC paralel berfungsi seperti rangkaian terbuka dengan arus rangkaian
ditentukan oleh resistor, hanya R. Jadi total impedansi dari rangkaian
resonansi paralel pada resonansi hanya menjadi nilai resistansi dalam rangkaian
dan Z = R seperti yang ditunjukkan.
Dengan demikian pada resonansi, impedansi dari
rangkaian paralel berada pada nilai maksimum dan sama dengan resistansi dari
rangkaian yang menciptakan kondisi rangkaian dengan resistansi tinggi dan arus
rendah. Juga di resonansi, sebagai impedansi dari rangkaian tersebut adalah
sekarang bahwa resistansi saja, total arus, I akan “dalam-fasa” dengan tegangan
supply, VS.
Kita dapat mengubah respons frekuensi rangkaian
dengan mengubah nilai resistansi ini. Mengubah nilai R mempengaruhi jumlah arus
yang mengalir melalui rangkaian pada resonansi, jika L dan C tetap konstan.
Kemudian impedansi rangkaian pada resonansi Z = RMAX disebut
"impedansi dinamis" rangkaian.
Impedansi dalam Rangkaian Resonansi Paralel
Perhatikan bahwa jika impedansi rangkaian
paralel maksimum pada resonansi maka konsekuensinya, admitansi rangkaian harus
minimum dan salah satu karakteristik rangkaian resonansi paralel adalah
admitansi/penerimaannya sangat rendah sehingga membatasi arus rangkaian.
Berbeda dengan rangkaian resonansi seri, resistor dalam rangkaian resonansi
paralel memiliki efek redaman pada bandwidth bandwidth yang membuat rangkaian
kurang selektif.
Juga, karena arus rangkaian konstan untuk nilai
impedansi apa pun, Z, tegangan melintasi rangkaian resonansi paralel akan
memiliki bentuk yang sama dengan impedansi total dan untuk rangkaian paralel,
bentuk gelombang tegangan umumnya diambil dari kapasitor.
Kita sekarang tahu bahwa pada frekuensi resonansi, ƒr yang masuk dari rangkaian tersebut adalah minimal dan sama dengan konduktansi, G diberikan oleh 1/R karena dalam rangkaian resonansi paralel bagian imajiner dari admitansi, yaitu susceptance, B adalah nol karena BL = BC seperti yang ditunjukkan
Susceptansi pada Resonansi
Dari atas, Susceptansi atau kerentanan induktif
, BL berbanding
terbalik dengan frekuensi yang diwakili oleh kurva hiperbolik. Susceptansi
kapasitif , BC berbanding
lurus dengan frekuensi dan karena itu diwakili oleh garis lurus.
Kurva terakhir menunjukkan plot susceptansi
total dari rangkaian resonansi paralel versus frekuensi dan merupakan perbedaan
antara kedua susceptansi itu. Kemudian kita dapat melihat bahwa pada titik
frekuensi resonansi jika melintasi sumbu horizontal, susunan total rangkaian
adalah nol.
Di bawah titik frekuensi resonansi, susceptansi
induktif mendominasi rangkaian yang menghasilkan faktor daya
"lagging", sedangkan di atas titik frekuensi resonansi, susceptansi
kapasitif mendominasi yang menghasilkan faktor daya "lead".
Jadi pada frekuensi resonansi, atau arus yang diambil
dari supply harus “in-phase” dengan tegangan yang diterapkan secara
efektif hanya ada resistansi yang ada dalam rangkaian paralel, sehingga faktor
daya menjadi satu atau kesatuan, ( θ = 0° ).
Juga karena impedansi rangkaian paralel berubah
dengan frekuensi, ini membuat impedansi rangkaian “dinamis” dengan arus pada
resonansi berada dalam-fasa dengan tegangan karena impedansi rangkaian
bertindak sebagai hambatan. Kemudian kita telah melihat bahwa impedansi dari
rangkaian paralel pada resonansi setara dengan nilai resistansi dan nilai ini
harus, oleh karena itu mewakili impedansi dinamis maksimum ( Zd ) dari rangkaian seperti yang
ditunjukkan.
Arus dalam Rangkaian Resonansi Paralel
Sebagai total susceptansi adalah nol pada frekuensi
resonansi, admitansi adalah minimal dan sama dengan konduktansi, G. Oleh karena
itu pada resonansi arus yang mengalir melalui rangkaian juga harus minimum
karena arus cabang induktif dan kapasitif sama ( IL = IC ) dan berada diluar-fasa 180°.
Kita ingat bahwa arus total yang mengalir dalam
rangkaian RLC paralel sama dengan jumlah vektor arus cabang individu dan untuk
frekuensi tertentu dihitung sebagai:
Pada resonansi, arus IL dan IC sama dan membatalkan sehingga
memberikan arus reaktif bersih sama dengan nol. Kemudian pada resonansi
persamaan di atas menjadi.
Karena arus yang mengalir melalui rangkaian resonansi paralel adalah hasil dari tegangan dibagi dengan impedansi, pada resonansi impedansi, Z berada pada nilai maksimumnya, ( = R ). Oleh karena itu, arus rangkaian pada frekuensi ini akan berada pada nilai minimum V/R dan grafik arus terhadap frekuensi untuk rangkaian resonansi paralel diberikan sebagai.
Arus Rangkaian Paralel dengan Resonansi
Kurva respons frekuensi dari rangkaian resonansi
paralel menunjukkan bahwa besarnya arus adalah fungsi frekuensi dan memplotnya
ke grafik menunjukkan kepada kita bahwa respons dimulai dari nilai maksimumnya,
mencapai nilai minimumnya pada frekuensi resonansi ketika IMIN = IR dan kemudian meningkat lagi menjadi
maksimum ketika ƒ menjadi tidak terbatas.
Hasil dari ini adalah bahwa besarnya arus yang
mengalir melalui induktor, L dan kapasitor, rangkaian tangki C dapat menjadi
beberapa kali lebih besar dari arus supply, bahkan pada resonansi tetapi karena
mereka sama dan pada resistansi (180° out-of-phase) mereka secara efektif
membatalkan satu sama lain.
Karena rangkaian resonansi paralel hanya
berfungsi pada frekuensi resonansi, tipe rangkaian ini juga dikenal sebagai
Rangkaian Rejecter karena pada resonansi, impedansi rangkaian berada pada batas
maksimum sehingga menekan atau menolak arus yang frekuensinya sama dengan
frekuensi resonansinya. Efek resonansi dalam rangkaian paralel juga disebut
"resonansi arus".
Perhitungan dan grafik yang digunakan di atas
untuk mendefinisikan rangkaian resonansi paralel mirip dengan yang kami gunakan
untuk rangkaian seri. Namun, karakteristik dan grafik yang digambar untuk
rangkaian paralel persis berlawanan dengan rangkaian seri dengan maksimum dan
minimum impedansi, arus dan perbesaran rangkaian terbalik. Itulah sebabnya
rangkaian resonansi paralel juga disebut rangkaian Anti-resonansi .
Bandwidth & Selektivitas Rangkian Resonansi Paralel
Bandwidth dari rangkaian resonansi paralel didefinisikan
dengan cara yang persis sama seperti untuk rangkaian resonansi seri. Frekuensi
cut-off atas dan bawah diberikan sebagai: ƒatas dan ƒbawah masing-masing menunjukkan frekuensi
setengah daya.
Di mana daya yang dihamburkan dalam rangkaian adalah setengah
dari daya penuh yang dihamburkan pada frekuensi resonansi 0.5 (I2R) yang memberi kita titik -3dB yang sama pada
nilai arus yang sama dengan 70.7% dari nilai resonansi maksimumnya, (0.707 x I)2R
Seperti rangkaian seri, jika frekuensi resonansi
tetap konstan, peningkatan dalam faktor kualitas, Q akan menyebabkan penurunan
bandwidth dan juga, penurunan faktor kualitas akan menyebabkan peningkatan
bandwidth seperti yang didefinisikan oleh:
BW = ƒr /Q atau BW = ƒatas dan ƒbawah
Juga mengubah rasio antara induktor, L dan
kapasitor, C, atau nilai resistansi, R bandwidth dan karenanya respon frekuensi
rangkaian akan diubah untuk frekuensi resonansi tetap. Teknik ini digunakan
secara luas dalam rangkaian tuning untuk pemancar dan penerima radio dan
televisi.
Selektivitas atau faktor-Q untuk rangkaian
resonansi paralel umumnya didefinisikan sebagai rasio arus cabang yang
bersirkulasi terhadap arus supply dan diberikan sebagai:
Perhatikan bahwa faktor-Q dari rangkaian
resonansi paralel adalah kebalikan dari ekspresi untuk faktor-Q dari rangkaian
seri. Juga dalam rangkaian resonansi seri, faktor-Q memberikan pembesaran
tegangan dari rangkaian, sedangkan pada rangkaian paralel memberikan pembesaran
arus.
Bandwidth dari Rangkaian Resonansi Paralel
https://abdulelektro.blogspot.com/2019/06/rangkaian-resonansi-seri.html
https://abdulelektro.blogspot.com/2019/06/rangkaian-resonansi-paralel.html


















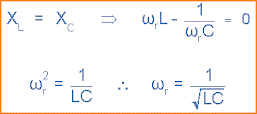



















saya muhammad reza pahlevi izin bertanya
BalasHapusyang dimaksud impedansi rangkaian dinamis itu apa sih?
saya Salsha Afifa izin menjawab, impedansi rangkaian dinamis itu jumlah hambatan listrik yang bisa berubah seiring dengan perubahan frekuensi sinyal
HapusKomentar ini telah dihapus oleh pengarang.
HapusSaya Marsel Ristian dari kelompok 4 ingin bertanya. Apakah syarat terjadinya resonansi harus dengan sumber tegangan AC..? Apa alasannya..? Terimakasih
BalasHapus